Dit is een van de beroemdste getallenreeksen in de wiskunde. De rij van Fibonacci is een reeks van getallen waarbij ieder getal in deze reeks de som is van de 2 voorgaande getallen. De eerste 2 getallen van de Fibonacci reeks zijn 0 en 1, daarnaast is deze Fibonacci reeks oneindig lang.
De rij van Fibonacci werd voor het eerst benoemd in 1202 in het boek Liber abaci. Dit boek werd geschreven door Leonardo van Pisa die als bijnaam Fibonacci had, vanwaar ook de naam voor deze reeks is afgeleid.
De Fibonacci-code is gebaseerd op de getallen in de rij van Fibonacci. Deze code gaat positieve gehele getallen omzetten in binaire code. Elk positief geheel getal kan geschreven worden als een som van getallen uit de Fibonacci reeks. Degene die je gebruikt zet je om naar 1 en degen die je niet gebruikt zet je om naar 0.
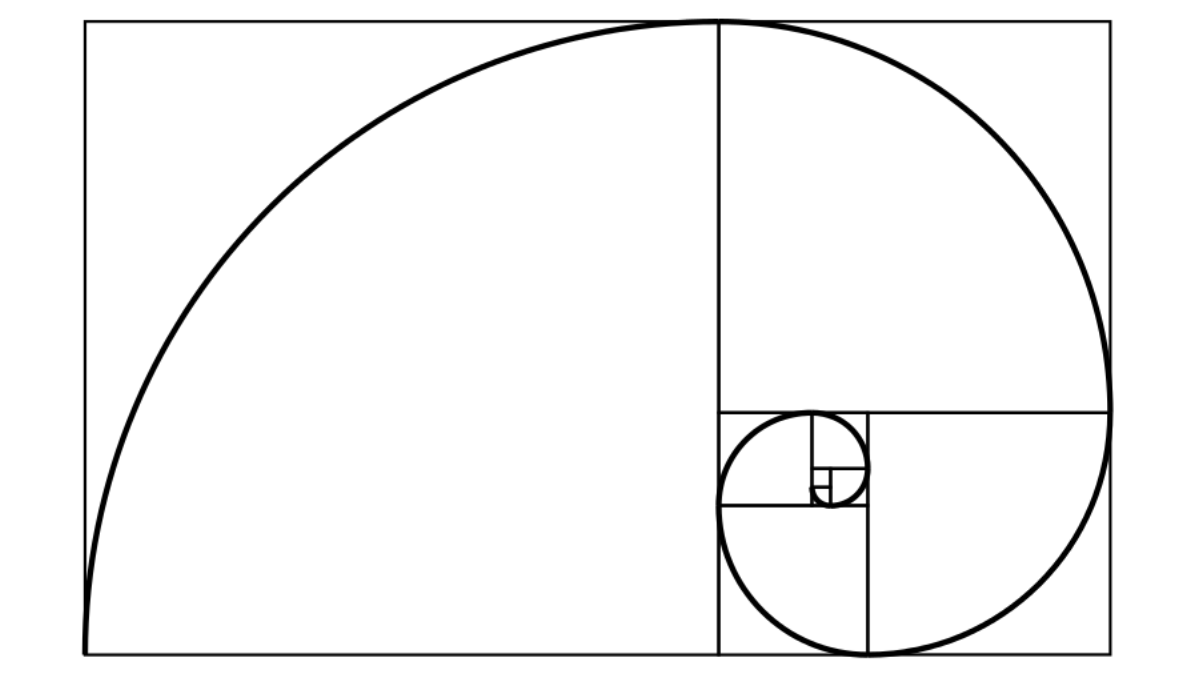
Wanneer je re Fibonacci reeks zou voorstellen als vierkanten, dan moet de zijde van een vierkant gelijk zijn aan de som van de zijdes van de 2 voorgaande vierkanten. Wanneer je deze vierkanten met 1 lijn verbindt, krijg je de Fibonacci spiraal die oneindig lang is.
Rij van Fibonacci: lijst met eerste 50 Fibonacci getallen
Hieronder kan je de eerste 50 getallen van de reeks van Fibonacci terugvinden. De rij start met 0 en 1 en vanf dan is elk getal uit de rij van Fibonacci de som van de voorgaande 2 getallen. Opvallend is dat je heel snel opbouwt tot grote getallen: het 50ste getal uit de Fibonacci reeks bestaat reeds uit 10 cijfers!
| 0 | 1 | 1 |
| 2 | 3 | 5 |
| 8 | 13 | 21 |
| 34 | 55 | 89 |
| 144 | 233 | 377 |
| 610 | 987 | 1597 |
| 2584 | 4181 | 6765 |
| 10946 | 17711 | 28657 |
| 46368 | 75025 | 121393 |
| 196418 | 317811 | 514229 |
| 832040 | 1346269 | 2178309 |
| 3524578 | 5702887 | 9227465 |
| 14930352 | 24157817 | 39088169 |
| 63245986 | 102334155 | 165580141 |
| 267914296 | 433494437 | 701408733 |
| 1134903170 | 1836311903 | 2971215073 |
| 4807526976 | 7778742049 |
Fibonacci code
De Fibonacci-code is een code die gebruikt wordt in de Informatica en gebaseerd is op de rij van Fibonacci. Deze Fibonacci code gaat positieve gehele getallen coderen tot binaire woorden. Om de Fibonacci code te bepalen, moet je ervan uitgaan dat ieder geheel getal kan geschreven worden als een som van getallen uit de Fibonacci reeks. Belangrijk om weten is dat iedere Fibonacci code eindigt op een 1 (die je altijd extra moet toevoegen).
Voorbeeld: 12 = 1 + 3 + 8
Wanneer je de Fibonacci reeks uitschrijft zonder de eerste 2 getallen, dan heb je dit:
1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, …
Wanneer je nu ieder getal dat je gebruikt van de Fibonacci reeks in je som vervangt door een 1 en de andere door 0, bekom je voor ieder getal de Fibonacci code (vergeet de laatste 1 niet extra toe te voegen!).
Zo kan je 12 omzetten naar Fibonacci code: 101011
Lijst van Fibonacci-code
Hieronder kan je de eerste 20 getallen in Fibonacci-code terugvinden.
| 1 | 11 | 11 | 001011 |
| 2 | 011 | 12 | 101011 |
| 3 | 0011 | 13 | 0000011 |
| 4 | 1011 | 14 | 1000011 |
| 5 | 00011 | 15 | 0100011 |
| 6 | 10011 | 16 | 0010011 |
| 7 | 01011 | 17 | 1010011 |
| 8 | 000011 | 18 | 0001011 |
| 9 | 100011 | 19 | 1001011 |
| 10 | 010011 | 20 | 0101011 |
Rij van Lucas
De rij van Fibonacci heeft een variant in de vorm van de rij van Lucas: deze getallenreeks wordt op dezelfde manier gevormd, maar met andere startwaarden.